aman9das - Estimating Meridian Length

In this article, we will try to estimate the length of the Earth’s Meridian.

Theory

In 1687, Isaac Newton claimed that the Earths rotation around its axis made it an Oblate Sphere. Rotation caused flattening at the Poles and bulging at the Equator.

If so, the distance (on earths surface) between two Latitude lines would be: \[ Y \approx C + m\sin^2\theta \]

Where \(\theta\) is the central meridian angle and \(C\) and \(m\) are unknown parameters of the Earth.

We may interpret \(Y\) to be a dependent variable on \(\sin^2\theta\) and estimate \(C\), and \(m\). Thus we can estimate the whole meridian length by summing over the latitude angles using regression.

We will make use of two historical data sets for this article.

Import dataset

We store the data in an Open Document Foundation Spreadsheet geodata#.ods.

Code

library(readODS)

d1 = read_ods("geodata1.ods")
d2 = read_ods("geodata2.ods")

Standardization

We standardize X and set Y to sin²θ and meter.

Code

radians = function(degree, minute = 0, second = 0){
  ratiod = pi / 180
  ratiom = ratiod / 60
  ratios = ratiom / 60
  res = degree * ratiod + minute * ratiom + second * ratios
  return(res)
}

d1$lat = radians(d1$lat1, d1$lat2)
d1$X = (sin(d1$lat))^2
d1$Y = d1$arc * 6.39 * 0.3048

d2$lat = radians(d2$L1, d2$L2, d2$L3)
d2$arc = d2$S / d2$d
d2$X = (sin(d2$lat))^2
d2$Y = d2$arc * 12.78 * 0.3048

Out dataset looks like this at this point:

Code

d1

# A tibble: 5 × 7
   lat1  lat2   arc  sin2   lat     X       Y
  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>   <dbl>
1     0     0 56751     0 0     0     110532.
2    33    18 57037  3014 0.581 0.301 111089.
3    42    59 56979  4648 0.750 0.465 110976.
4    49    23 57074  5762 0.862 0.576 111161.
5    66    19 57422  8386 1.16  0.839 111839.

Code

d2

# A tibble: 4 × 9
       S     d    L1    L2    L3   lat    arc     X       Y
   <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl> <dbl>   <dbl>
1 62473.  2.19    49    56    30 0.872 28538. 0.586 111165.
2 76546.  2.67    47    30    46 0.829 28683. 0.544 111730.
3 84425.  2.96    44    41    48 0.780 28489. 0.495 110976.
4 52749.  1.85    42    17    20 0.738 28472. 0.453 110909.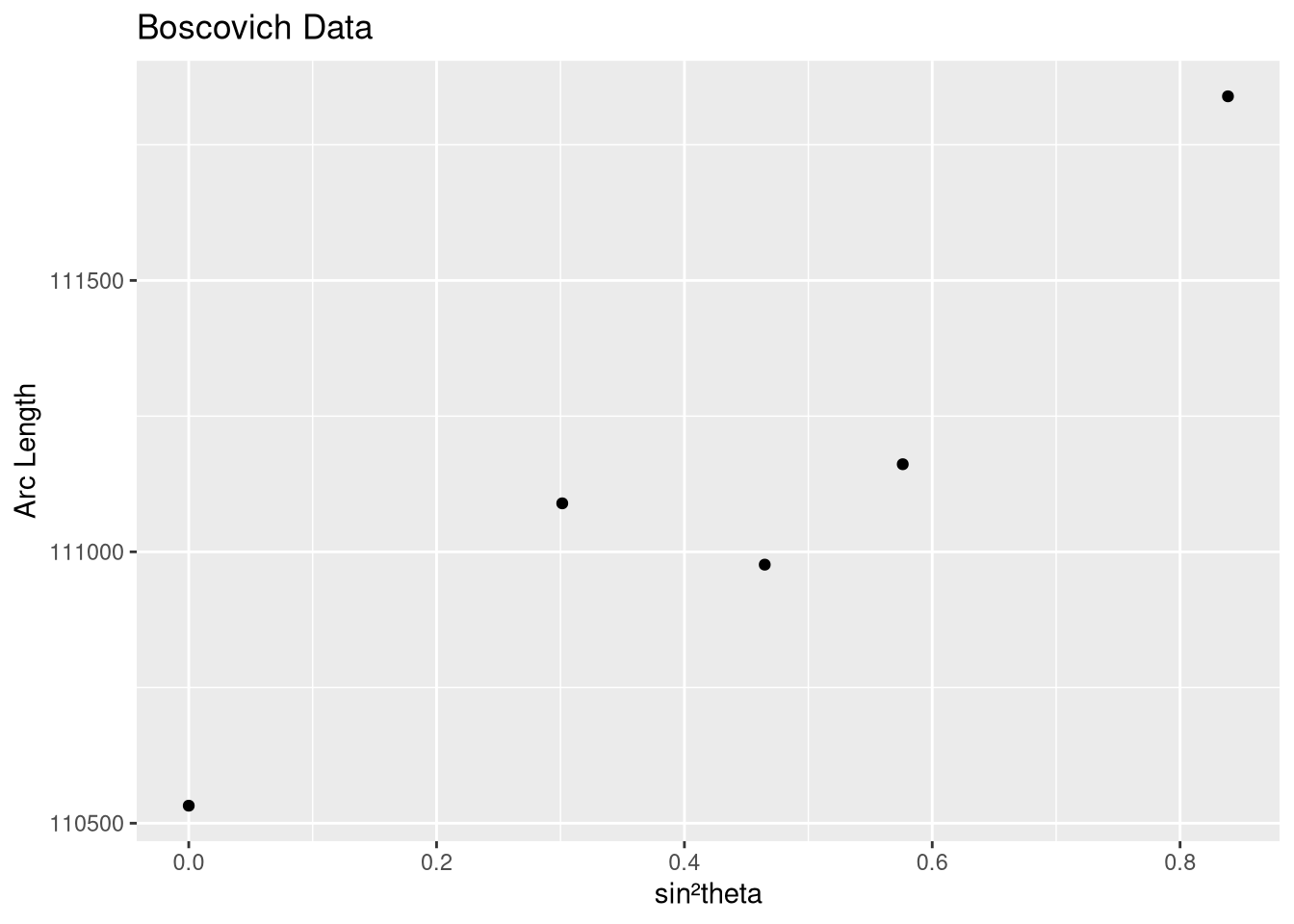

Plot the data

Code

library(ggplot2)

ggplot(d1, aes(x = X, y = Y))+
  geom_point()+
  labs(title = "Boscovich Data", )+xlab("sin²theta")+ylab("Arc Length")

Code

ggplot(d2, aes(x = X, y = Y))+
  geom_point()+
  labs(title = "French Data", )+xlab("sin²theta")+ylab("Arc Length")

Ordinary Least Squares Estimate

Estimate the coefficient of sin²θ and Intercept using Least Squares Estimate. And Predict Meridian Length.

Code

estmerlen = function(coeff){ as.numeric( coeff[1]*90 + coeff[2]*45 ) }

olsmodel1 = lm(formula=d1$Y~d1$X)
cat( "Boscovich Data OLS estimate of Meridian Line length:",  estmerlen(olsmodel1$coefficients) )

Boscovich Data OLS estimate of Meridian Line length: 10008879

Code

olsmodel2 = lm(formula=d2$Y~d2$X)
cat( "French Data OLS estimate of Meridian Line length:",  estmerlen(olsmodel2$coefficients) )

French Data OLS estimate of Meridian Line length: 10001451

Least Absolute Deviation Estimation

Estimate the coefficient of sin²θ and Intercept using Least Absolute Deviation. Elemental Lines were used to compute LAD. Predict Meridian Length.

Elemental Lines are lines joining two data points in the Sample Space.

Code

ad = function(Y, X, a, b){
  l = length(Y)
  cumudevn = 0
  for (i in seq(l)) {
    devn = abs( Y[i] - a - b * X[i] )
    cumudevn = cumudevn + devn
  }
  
  return(cumudevn)
}

lad = function(Y, X){
  l = length(Y)
  labsdevn = sum( abs(Y - mean(Y)) )
  coeff = c( mean(Y), 0)
  for (i in seq(l-1)) {
    for (j in seq(i+1, l)) {
      b1 = (Y[j] - Y[i])/(X[j] - X[i])
      b0 = (Y[i] - b1 * X[i])
      absdevn = ad(Y, X, b0, b1)
      if (labsdevn > absdevn) {
        labsdevn = absdevn
        coeff = c(b0, b1)
      }
    }
  }
  
  return(coeff)
}

ladmodel1 = lad(d1$Y, d1$X)
cat( "Boscovich Data LAD estimate of Meridian Line length:",  estmerlen(ladmodel1) )

Boscovich Data LAD estimate of Meridian Line length: 10018034

Code

ladmodel2 = lad(d2$Y, d2$X)
cat( "French Data LAD estimate of Meridian Line length:",  estmerlen(ladmodel2) )

French Data LAD estimate of Meridian Line length: 9990026

Conclusion

Both OLS and LAD models predict the Meridian length to be close to ten million meters. Hence the meter as prescribed at the time, was close to the intended definition.